
遗传算法(Genetic Algorithm, GA)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。其主要特点是直接对结构对象进行操作,不存在求导和函数连续性的限定;具有内在的隐并行性和更好的全局寻优能力;采用概率化的寻优方法,不需要确定的规则就能自动获取和指导优化的搜索空间,自适应地调整搜索方向。遗传算法以一种群体中的所有个体为对象,并利用随机化技术指导对一个被编码的参数空间进行高效搜索。其中,选择、交叉和变异构成了遗传算法的遗传操作;参数编码、初始群体的设定、适应度函数的设计、遗传操作设计、控制参数设定五个要素组成了遗传算法的核心内容。
遗传算法能够自我迭代,让它本身系统内的东西进行优胜劣汰的自然选择,把好的保留下来,次一点的东西就排除掉。遗传算法的本质就是是优胜劣汰,选出最优秀的个体,一般用来寻找最优解。
一次迭代包括以下几个过程:

既然是应用,我直接举个例子,我觉得更容易理解,比如我现在需要求z=f(x,y)在x,y取值范围为(0,20)时的最大值。简单的函数可以手动求,但是假如是下图这样的呢?
Z =sin(X)+cos(Y)+0.1X+0.1Y


首先,既然是遗传,寻找最优解,可以理解成找到最好的一个个体,那就得在一定的个体中去实现。这些所有的个体就构成了一个种群。在仿真中,自己规定种群的大小,比如z=f(x,y)的种群大小是N,也就是N个个体,它的意思就是在自变量的取值范围内随机取N个值,也就有N个函数值了。种群包含个体
在一个种群中,有若干的个体,他们有着不同的特征。比如z1=f(x1,y1)就是一个个体,具体到自变量取了确定值后,这个个体也就所有信息都知道了。个体包含染色体和适应度
一个个体对应一个染色体,染色体是个体基因的总称,比如z=f(x,y)中(x1,y1)就是其中的一个染色体。染色体包含基因
一个个体对应一个染色体,但是可以有多个基因。其实就是一个函数的多个自变量,比如z=f(x,y),则称该个体有2个基因。基因就是自变量
一个个体在基因确定的情况下,它的适应度就确定了。比如z1=f(x1,y1),则z1的值就是该个体的适应度。适应度就是确定自变量后对应的函数值
染色体的交叉:N个染色体中,任意两个可能会交换染色体的某一部分基因。以一定概率通过互换两个父代个体的部分染色体产生新个体的运算。交叉运算是遗传算法核心算法之一,该算法在遗传过程中使用的频率最高,其目的是基于优良父代基因的基础上进一步扩展有限个体的覆盖面积。种群的发展影响着环境,环境也在选择适合生存的个体。
染色体的变异:在发展的过程中,染色体自身可能发生某种突变,这里仅仅考虑某个基因的随机改变。将某一父代个体基因链的某些基因座上的基因值以某一概率作变动,形成新个体的运算。变异运算同样是遗传算法核心算法之一,旨在跳出局部搜索范畴,体现全区搜索的思想。
优胜劣汰,自然选择。
建立在群体中个体的适应度评估基础上,将适应度值高的个体直接遗传到下一代或者通过交叉算子和变异算子产生新个体后再遗传到下一代。
我试过两种方法:
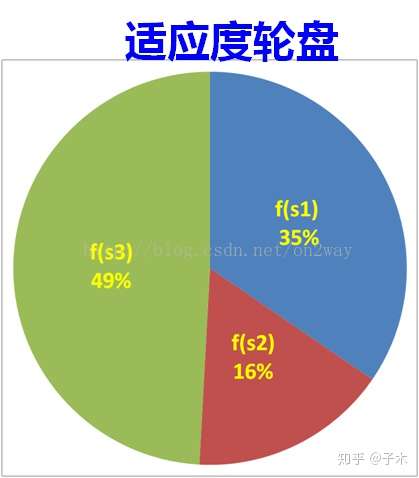
原理是按照某个体的适应度在总适应度中的贡献来确定是否选择它,为技术的发展做出过贡献的老板,人们是不会忘记他的
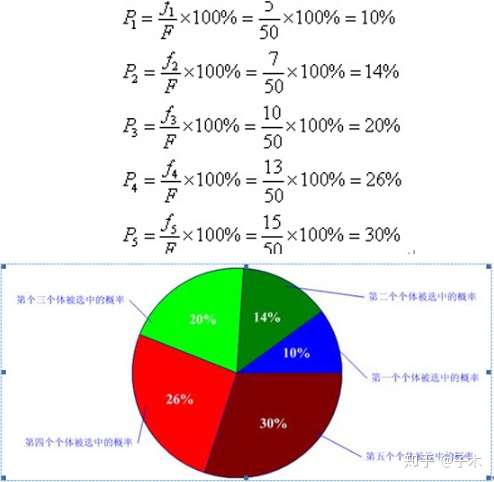
随便举个例子吧,假如算出的N个适应度分别是[1,3,5,9,7,6,8,2,8,7......8,7,3,8],对其按升序排列,并依次求和,则所求的适应度之和也是升序排列。假如总适应度是M(对所有适应度求和)并比喻作整个轮盘。现在某种群发展协会召集所有个体来开一个会,干什么的呢?
选出对技术发展做出过突出贡献的人,并赋予它们交配权,被我选中的人,你就可以拥有后代啦ヾ(゚∀゚ゞ)。
规则是什么呢?
按照你们N个个体的贡献度从小到大排好序,你们每个人手里有一个数字,他是你及你以前所有个体的贡献度之和。挨个上台抽签,盒子里装有N个数,分别是比适应度总和小的任意值,个体上台之后从盒子里抽一个数,如果抽到的数比手里的数小的话,恭喜你,进入下一轮。
所以适应度大的染色体有更大的概率被选中,这么说吧,假如某个个体的贡献度是8,适应度总和是10,那是不是只要抽到的数大于2的,这个个体就稳了呢。
那么如何实现轮盘赌法呢,具体参考程序。
覆盖法就很粗暴了,直接用最优的覆盖掉交叉的,比如把适应度序列后面百分之20直接用最优的染色体覆盖。强者不但拥有交配权,还可以多生,多生,多生ヽ(°▽、°)ノ。
**比较:**我个人的理解是
选择轮盘赌法的原因是某个染色体这一代的适应度不好,但是有可能通过染色体变异和交叉后,下一代的适应度很好呢。所以采用概率的方式,不能一竿子把适应度差的全打倒。三十年河东,三十年河西,莫欺少年。。。。基因差?
5.另外一个概念就是编码
染色体实为要问题的解,如图 所示,是染色体的基本结构,其中基因位位数和基因位的值需要根据不同的问题来进行相应的设计。为了方便计算,我们在解决问题的时候都是采用的二进制编码,因此,每个基因位的取值都为 0或 1。
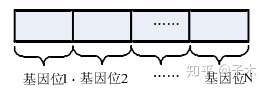
此外,染色体的编码方式还有格雷码、浮点数编码等,基因位也要根据问题的不同来进行相应的基因位长度设计,一般在进行问题的设计的时候都尽量将问题的解的取值设计成 2的 N 次方,这样基因位的长度一般都取 N,方便问题的解决。灵活的进行染色体的设计,可使得遗传算法更快的得到问题的解。
我使用的是二进制编码方式
实数编码:直接用实数表示基因,容易理解且不需要解码过程,但容易过早收敛,从而陷入局部最优
二进制编码:稳定性高,种群多样性大,但需要的存储空间大,需要解码且难以理解
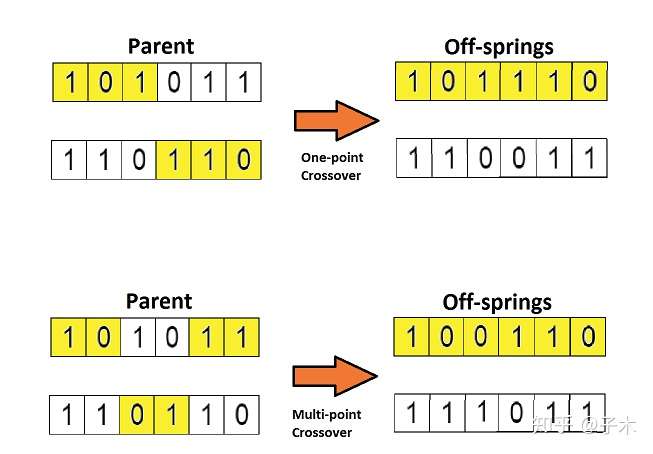
变异、交叉容易理解
二进制编码的缺点是:对于一些连续函数的优化问题,由于其随机性使得其局部搜索能力较差,如对于一些高精度的问题(如上题),当解迫近于最优解后,由于其变异后表现型变化很大,不连续,所以会远离最优解,达不到稳定
编码(coding):DNA中遗传信息在一个长链上按一定的模式排列。遗传编码可看作从表现型到基因型的映射。
解码(decoding):基因型到表现型的映射。
大概概念也就这些,具体的还是结合程序看。
遗传算法并不保证你能获得问题的最优解,但是使用遗传算法的最大优点在于你不必去了解和操心如何去“找”最优解。而只要简单的“否定”一些表现不好的个体就行了。这就是遗传算法的精粹!
上一期介绍了遗传算法求解线性规划的问题。我们来看看下面这个例子,能否用上次讲的方法解决。

上述例子,第二个约束条件含有二次项,并不是线性的,用上次的方法好像无法直接解决。下面我们就来介绍一下非线性规划的遗传算法的实现。
和线性规划一样,在调用遗传算法工具箱之前,也得学习一下非线性规划的标准形式。因为,调用工具箱需要我们将非标准形式的模型转化为标准形式。

其中,是目标函数,线性或者非线性都可以。式[1]、式[2]、式[5]同线性规划,为相应维数的矩阵和向量。式[3]表示非线性的不等式约束,式[4]是非线性等式约束。和为非线性向量函数(这里可能不好理解,下面结合一个例子解释)
例如以下模型

可以看出,这个模型没有线性约束,式[1]、式[2]、式[3]、式[4]均为非线性的。其中,式[1]、式[2]是非线性不等式约束,式[3]、式[4]是等式约束。对于非标准的非线性规划模型,我们先得化为标准的模型,转化方式和线性规划相同,采用添负号或者乘-1的方式。

注意到这里的 应是一个向量函数,本模型中有两个不等式约束,函数 的返回值应该是两个数。(看不懂没关系,编程时会具体讲解如何编写)

注意到这里的 应是一个向量函数,本模型中有两个等式约束,函数 的返回值应该式是两个数。(看不懂没关系,编程时会具体讲解如何编写)
MATLAB提供的遗传算法工具箱,主要分为两个函数:gaoptimset()函数和ga()函数,gaoptimset()函数是用于设置遗传算法的一些参数的,可以不设置。若不设置,就使用默认参数。ga()函数是调用遗传算法对优化问题进行计算。
调用格式为: options = gaoptimset('Param1', value1, 'Param2', value2, ...);
其中,'Param1'、'Param2'等是需要设定的参数,比如:种群规模、交叉比例等。value1、value2等则是Param的具体值。常用的参数名如下表(只列出了常用的,还有很多参数可以调整,可自行上网搜索):

例如,需要设置交叉比例为0.7、迭代次数为300、种群规模为30,代码写作
options = gaoptimset('CrossoverFraction', 0.7, 'Generations', 300, 'PopulationSize', 30);
返回的options是结构体,用于ga函数的最后一个参数
ga函数的调用格式为:
[x_best,fval] = ga(fun, nvars, A, b, Aeq, beq, lb, ub, nonlcon, options);

返回值x_best为取到最小值时的自变量x的取值,fval为所求的最小值。


目标函数的编写就不多说了,和之前线性规划的编写方法相同
function f = fitnessfun(x)
f = x(1)^2 + x(2)^2 + x(3)^3 + 8;
end